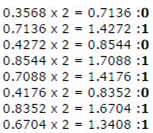Fixed Point Numbers
The Binary Point
Fixed Point numbers are a straightforward and simple approach to express Fractional numbers, utilizing a Fixed Number of bits.
The expression "Fixed Point" alludes to the position of the Binary Point. The Binary Point is similar to the Decimal Point of a base-ten number, however since this is Binary as opposed to Decimal, an alternate term is utilized. In Binary, bits can be either 0 or 1 and there is no different image to assign where the Binary Point lies. Be that as it may, we envision, or accept, that the Binary Point lives at a Fixed area between assigned bits in the number.
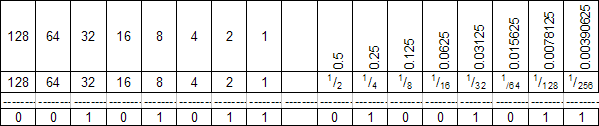
For example, in a 32-bit number, we can expect that the Binary Point exists specifically between bits 15 (15 in light of the fact that the primary piece is numbered 0, not 1) and 16, giving 16 bits for the Whole number part and 16 bits for the Fractional part. Note that the most significant bit in the whole number field is generally designated as the sign bit leaving 15 bits for the whole number's magnitude.
Place Value Method
Not all numbers can be represented exactly by a fixed-point number, and so the closest approximation is used.
In the above example the number stored would be :
32 + 8 + 2 + 1 + 0.25 + 0.03125 + 0.0078125 + 0.00390625 = 43.2869375
Repeated Multiplication
You can convert any decimal fraction to a binary fraction. Multiply the fractional part of the number by 2. Take the integer part of the result (1 or 0) as the first bit. Repeat this process with the result until you run out of patience. For example, to convert 0.3568 into fixed point binary with 8 bits to the right of the binary point,
0.3568 is .01011011