Difference between revisions of "BNF - Syntax Diagrams"
(→Quiz) |
|||
| (16 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | ==Overview== |
<youtube>https://www.youtube.com/watch?v=x1gGInKNCRw&list=PLCiOXwirraUAnbNTfWFxkoq5MoIair49B&index=6</youtube> | <youtube>https://www.youtube.com/watch?v=x1gGInKNCRw&list=PLCiOXwirraUAnbNTfWFxkoq5MoIair49B&index=6</youtube> | ||
| Line 6: | Line 6: | ||
==BNF== | ==BNF== | ||
| − | Backus Naur Form is a way of describing the syntax of a | + | Backus Naur Form is a way of describing the syntax of a of a language. |
| − | |||
| − | |||
| − | |||
| − | + | The symbols used are: | |
| − | |||
| − | |||
| − | ==''' | + | ::= is defined as |
| − | + | ||
| + | | or | ||
| + | |||
| + | < > meta variables or syntactic variables (non-terminal symbols) | ||
| + | |||
| + | For example a numerical digit could be defined as: | ||
| + | |||
| + | <digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| + | |||
| + | This declares that <digit> can only be the numbers 0-9, specifically 0 OR 1 OR 2 OR 3 etc. These digits are also considered to be 'terminal' because they can not be broken down any further. 'A', 'B' , or 'C' would clearly be invalid digits. | ||
| + | |||
| + | The variables created can be used to define other variables for example: | ||
| + | |||
| + | <lesson> ::= A | B | C | ||
| + | <lesson code> ::= <lesson><digit> | ||
| + | |||
| + | This notation can also be recursive: | ||
| + | |||
| + | <integer> ::= <digit> | <digit><integer> | ||
| + | |||
| + | This states that an integer can be a digit or a digit followed by another integer. If the definition was just '<digit> <digit>' this would only allow integers of exactly 2 digits. | ||
==Syntax Diagrams== | ==Syntax Diagrams== | ||
| − | These are a diagram approach similar to BNF, they also describe the syntax allowed. | + | These are a diagram approach similar to BNF, they also describe the syntax allowed. |
| + | |||
| + | Instead of writing the you create diagrams and you are looking for path from left to right, some paths can loop back to allow for multiple digits. | ||
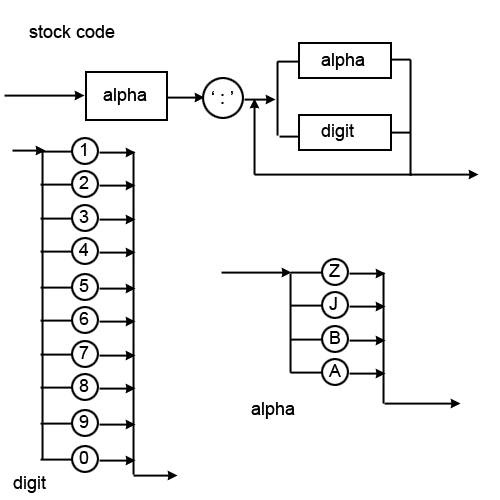
[[File:Syntaxdiagram.gif]] | [[File:Syntaxdiagram.gif]] | ||
| − | A recursive example: | + | The shape of the components are important: |
| + | * 'circle' is a literal character (ie it literally is the actual character contained within the circle). | ||
| + | * 'lozenge' is literal text (ie the exact text contained within the shape, it is not a variable name). | ||
| + | * 'rectangle' is used to enclose elements defined by other rules | ||
| + | |||
| + | so using this diagram, we can see that a digit can be 0-9, and alpha can only be A,B,J, or Z. A stock code must therefore start with one of the alpha characters and then followed by a colon. It can then have any combination of alpha characters or digit characters. Therefore a stock code starting 'AA:' will be invalid, as will a stock code starting '1:'. | ||
| + | |||
| + | You could also say the 'circle' & 'lozenge' are 'terminal' and the 'rectangle' is 'non-terminal'. | ||
| + | |||
| + | ===Recursive=== | ||
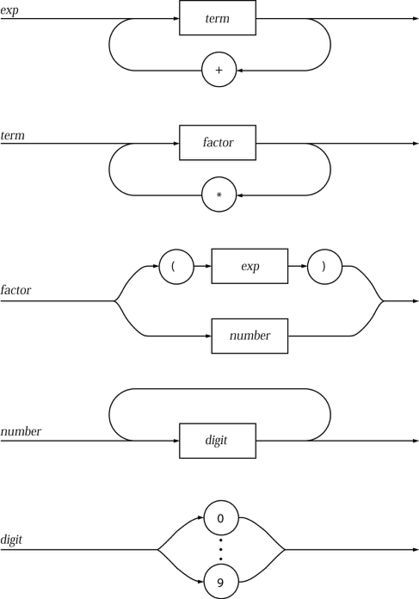
| + | It is unlikely that any syntax diagrams will be recursive, because BNF is recursive to cope with infinite sizes and syntax diagrams achieve this by using loop backs. However this is another example, this time it is recursive (factor uses exp as part of the diagram): | ||
[[File:Recursivesyntax.jpg]] | [[File:Recursivesyntax.jpg]] | ||
| + | |||
| + | Follow this example from the bottom up, starting at digit and then progress up the diagrams. | ||
Latest revision as of 08:47, 23 August 2023
Contents
Overview
https://www.youtube.com/watch?v=x1gGInKNCRw&list=PLCiOXwirraUAnbNTfWFxkoq5MoIair49B&index=6
BNF
Backus Naur Form is a way of describing the syntax of a of a language.
The symbols used are:
::= is defined as
| or
< > meta variables or syntactic variables (non-terminal symbols)
For example a numerical digit could be defined as:
<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
This declares that <digit> can only be the numbers 0-9, specifically 0 OR 1 OR 2 OR 3 etc. These digits are also considered to be 'terminal' because they can not be broken down any further. 'A', 'B' , or 'C' would clearly be invalid digits.
The variables created can be used to define other variables for example:
<lesson> ::= A | B | C <lesson code> ::= <lesson><digit>
This notation can also be recursive:
<integer> ::= <digit> | <digit><integer>
This states that an integer can be a digit or a digit followed by another integer. If the definition was just '<digit> <digit>' this would only allow integers of exactly 2 digits.
Syntax Diagrams
These are a diagram approach similar to BNF, they also describe the syntax allowed.
Instead of writing the you create diagrams and you are looking for path from left to right, some paths can loop back to allow for multiple digits.
The shape of the components are important:
- 'circle' is a literal character (ie it literally is the actual character contained within the circle).
- 'lozenge' is literal text (ie the exact text contained within the shape, it is not a variable name).
- 'rectangle' is used to enclose elements defined by other rules
so using this diagram, we can see that a digit can be 0-9, and alpha can only be A,B,J, or Z. A stock code must therefore start with one of the alpha characters and then followed by a colon. It can then have any combination of alpha characters or digit characters. Therefore a stock code starting 'AA:' will be invalid, as will a stock code starting '1:'.
You could also say the 'circle' & 'lozenge' are 'terminal' and the 'rectangle' is 'non-terminal'.
Recursive
It is unlikely that any syntax diagrams will be recursive, because BNF is recursive to cope with infinite sizes and syntax diagrams achieve this by using loop backs. However this is another example, this time it is recursive (factor uses exp as part of the diagram):
Follow this example from the bottom up, starting at digit and then progress up the diagrams.