Difference between revisions of "Addition"
(→Binary Addition) |
(→TRC PowerPoint) |
||
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | =Overview= | ||
| + | |||
| + | ===CraignDave=== | ||
| + | Addition is covered from 0:00 until 5:46 | ||
| + | |||
| + | <youtube>https://www.youtube.com/watch?v=t15dhDG_WUA&list=PLCiOXwirraUDGCeSoEPSN-e2o9exXdOka&index=2</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=t15dhDG_WUA&list=PLCiOXwirraUDGCeSoEPSN-e2o9exXdOka&index=2 (0:00 - 5:46) | ||
| + | |||
| + | ===Computer Science Tutor=== | ||
| + | <youtube>4wrBpIYimrw</youtube> | ||
| + | |||
| + | https://www.youtube.com/watch?v=4wrBpIYimrw&list=PL04uZ7242_M6O_6ITD6ncf7EonVHyBeCm&index=4 | ||
| + | |||
=Binary Addition= | =Binary Addition= | ||
Binary addition is being able to add two numbers together which are represented in binary form, which consist of 1s and 0s, you can add them together by converting them into denary, adding It together and then converting it back but its much faster to use the column addition method which you will see below. | Binary addition is being able to add two numbers together which are represented in binary form, which consist of 1s and 0s, you can add them together by converting them into denary, adding It together and then converting it back but its much faster to use the column addition method which you will see below. | ||
| Line 20: | Line 34: | ||
110 + | 110 + | ||
111 | 111 | ||
| − | + | --- | |
So: | So: | ||
0+1 = 1<br> | 0+1 = 1<br> | ||
| Line 36: | Line 50: | ||
For example: | For example: | ||
| − | + | 101 | |
| − | 101 | + | 101+ |
| − | + | 011+ | |
| − | 101 | + | ---- |
| − | |||
| − | 011+ | ||
Which would = 1101 | Which would = 1101 | ||
| − | + | If you do end up in a situation where you have more than 3 ones, you need to miss a column and place the carry in the next one. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=Revision= | =Revision= | ||
Latest revision as of 09:24, 25 September 2020
Contents
Overview
CraignDave
Addition is covered from 0:00 until 5:46
https://www.youtube.com/watch?v=t15dhDG_WUA&list=PLCiOXwirraUDGCeSoEPSN-e2o9exXdOka&index=2 (0:00 - 5:46)
Computer Science Tutor
https://www.youtube.com/watch?v=4wrBpIYimrw&list=PL04uZ7242_M6O_6ITD6ncf7EonVHyBeCm&index=4
Binary Addition
Binary addition is being able to add two numbers together which are represented in binary form, which consist of 1s and 0s, you can add them together by converting them into denary, adding It together and then converting it back but its much faster to use the column addition method which you will see below.
There are four possibilities when adding binary numbers, these possibilities are:
a total of 0 (0+0) put down 0 a total of 1 (1+0, 0+1 or 0+0+carried 1) put down 1 a total of 2 (1+1) put down 0, carry 1 a total of 3 (1+1+ carried 1) put down 1, carry 1
For example, solve 6+7 using binary addition:
First convert 6 and 7 from denary to binary using your preferred method
6 = 4+2+0 = 110 7 = 4+2+1 = 111
Then add them keeping in mind the 4 possibilities and add each digit together, starting on the right:
110 + 111 ---
So:
0+1 = 1
1+1 = 0 carry 1
1+1+ carried 1 = 1 carry 1
1 + 0 = 1
so 110+111 = 1101. Converting this number back to denary gives us an answer of 13.
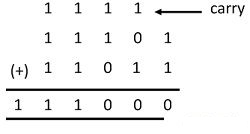
Another Example
Adding More Numbers Together
You could get 3 numbers to add however you wont be given a situation in which there are more than a total of 3.
For example:
101 101+ 011+ ----
Which would = 1101
If you do end up in a situation where you have more than 3 ones, you need to miss a column and place the carry in the next one.