Maths for Regular Expressions
Contents
Maths for Regular Expressions
https://www.youtube.com/watch?v=XfKOIWi420s&list=PLCiOXwirraUAnbNTfWFxkoq5MoIair49B&index=2
TRC Video
https://www.youtube.com/watch?v=R3rpZPpEA3k
Basic set understanding
Sets describe collections of things or values, such as numbers, animals or people.
In a set, each value occurs only once. For example, the value fox will occur only once in the set of animals. Just as the value 3 occurs only once in the element of all natural numbers, N.
The cardinality of a set refers to the number of elements it contains. An empty set is written ∅ and its cardinality is 0.
Sets may be finite or infinite. For example, the set of people currently alive in the world will be finite, but the set of N is infinite.
A set may be countable or uncountable. A countable set is a set, whose elements can be matched with the set of natural numbers. In other words, it is possible to count the elements one-by-one. If a set is finite, it will always be countable. The best example of an uncountable set is R. It is impossible to match each element of R with an element of N. This is because there are not enough elements in N to match each one with an element of R.
Membership ∈ and its reverse ∉
x ∈ S, x is an element of S.
Examples:
- x ∈ ℕ, meaning that x is an element of the set of natural numbers. For example, 3 ∈ ℕ. Whereas 3.5 ∉ ℕ
- x ∈ Q, meaning that x is an element of the set of rational numbers. Whereas pi ∉ Q
- x ∈ WorkingDays, meaning that x is an element of the set of all WorkingDays. For example, Monday ∈ WorkingDays. Whereas Saturday ∉ WorkingDays
- x ∈ WeekendDays, meaning that xis an element of the set of all WeekendDays. For example, Saturday ∈ WeekendDays. Whereas Monday ∉ WeekendDays
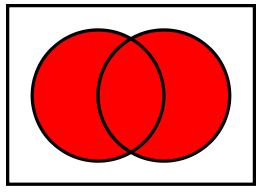
Union ∪
A ∪ B, meaning that all elements of the set A form a union with all of the elements in set B. This is a set comprehension, since this generates a new set.
The union of two sets:
Examples:
- Q ∪ Irrational Number Set, meaning that all numbers in the set of rational numbers form a union with the set of all irrational numbers. This set comprehension generates the set of real numbers.
- WorkingDays ∪ WeekendDays, meaning that all of the working days (elements of WorkingDays) form a union with weekend days (elements of WeekendDays). This set comprehension generates the set of WeekDays.
- {1, 2} ∪ {2,3,4} = {1,2,3,4} (notice that only once instance of 2 is in the resulting set)
- {1, 2, green} ∪ {red, white, green}={1, 2, red, white, green}
- {1, 2} ∪ {1, 2} = {1, 2}
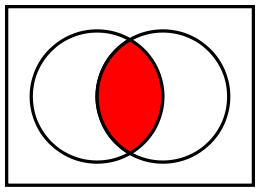
Intersection ∩
A ∩ B, meaning that the set A and set B form an intersection. The generated set will be ∅, if the two sets share no elements.
The intersection of two sets:
Examples:
Let A be the set of numbers which are divisible by 3 and B the set of numbers divisible by 4.
- A ∩ B, meaning that A and B form an intersection, which generates a set, which contains all of the numbers divisible by 3 and 4.
- WorkingDays ∩ WeekendDays, meaning that WorkingDays and WeekendDays form an intersection, which is ∅
Now let A be the set of all A-level students who take computer science and B the set of all A-level students who take mathematics.
- A ∩ B, meaning that A and B form an intersection, which generates a set, which contains all students who take both computer science and mathematics.
- {1, 2, 3} ∩ {2, 3, 4} = {2, 3}
- {1, 2, 3} ∩ {bear,hen,squirrel} = Ø (this means an empty set)
- {cat, dog, canary} ∩ {wolf, canary, whale, cat} = {cat, canary}
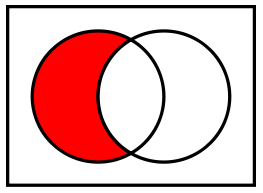
Difference \
A \ B, meaning that the set A and set B form a set difference. This will generate a set, which contains the elements of A, which are NOT also in B.
The difference of two sets:
Examples:
- R \ Q, meaning that R and Q form a set difference. This will generate the set of irrational numbers.
Let A be the set of all A-level students who take computer science and B the set of all A-level students who take mathematics.
- A \ B, meaning that A and B form a set difference. This will generate the set of all computer science students, who do not also take mathematics.
- {1, 2, 3} \ {2, 3, 4} = {1}
- {1, 2, 3} \ {bear,hen,squirrel} = {1, 2, 3}
- {cat, dog, canary} \ {wolf, canary, whale, cat} = {dog}
Proper Subsets ⊂
S ⊂ T, meaning that S is a proper subset of T, such that all elements in S are also elements of T. However, there will need to be at least one element in T, which is not in S. Examples:
- N ⊂ Z, meaning that the set of natural numbers is a proper subset of the set of integers. In other words, all natural numbers are also integers. There are some elements in Z, which are not in N - these are the negative integers.
- Z ⊂ Q, meaning that the set of integers is a proper subset of the set of rational numbers. In other words, all integers are also rational numbers. But there are rational numbers which are not integers.
Subsets ⊆
A ⊆ B, meaning that A forms a subset of B. In other words, A could be identical to B, but does not have to be! Examples: Let A be the set of all students in 6th form and B the set of all students taking computer science. ^A ⊆ B, meaning that A forms a subset of B. In other words, all students in the 6th form could be taking computer science. In which case the two sets would be the same, but they may not be! Now let A be all of the students present in school and B the set of students currently in the assembly hall.
- A ⊆ B, meaning that A forms a subset of B. In other words, all students currently in present in school may all be located in the assembly hall, but they may not be!
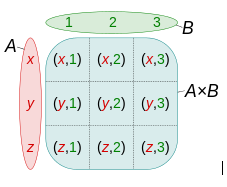
Cartesian Product
In mathematics, a Cartesian product is a mathematical operation that returns a set (or product set or simply product) from multiple sets. That is, for sets A and B, the Cartesian product A × B is the set of all ordered pairs (a, b) where a ∈ A and b ∈ B. The Cartesian Product of an empty set is an empty set. Products can be specified using set-builder notation, e.g.
Compact Set Notation
Compact set notation is a useful tool to describe the properties of each element of a set, rather than writing out all elements of a set. The table below lists all of the necessary symbols for compact set notation.
| Symbol | Meaning |
|---|---|
| x ∈ S | x is an element of S |
| | | such that |
| ∧ | and |
| ∨ | or |
| < | smaller than |
| <= | smaller or equal than |
| > | greater than |
| >= | greater or equal than |
| A ⊆ B | A is a subset of B |
| A ⊂ B | A is a proper subset of B |
| C = A ∪ B | C is the union of A and B |
| C = A ∩ B | C is the intersection of A and B |
| C = A \ B | C is the difference of A and B |
Example 1:
We might want to describe a set A, which contains all natural numbers greater than 10. This means that we are interested in a subset of ℕ, such that each of its elements is greater than the value 10. Using set notation this set can be described as:
A = {x|x ∈ ℕ ∧ x> 10}
Example 2:
This time set A is described as natural numbers, which are multiples of 10. This can be notated as:
A = {10x|x ∈ ℕ}
Example 3:
The elements of set A are all even numbers, up to including 12. Set notation allows us to write this set as {0,2,4,6,8,10,12}:
A = {2x | x ∈ N ∧ 2x < = 12}
If A is described as all even numbers, up to including 1,000,000:
A = {2x | x ∈ N ∧ 2x < = 1,000,000}
The table below explains how each expression is linked to the english description of the elements of the set A.
| English description... | ... expressed in set notation |
|---|---|
| 2 x | 2x |
| such that | | |
| x must be a natural number | x ∈ N |
| 2x must be smaller or equal than 1,000,000 | 2x < = 1,000,000 |
Example 4:
Set A is described as all the natural multiples of 3, below 5,000.
A = {3x | x ∈ N ∧ 3x > 5,000}
The table below explains how each expression is linked to the english description of the elements of the set A.
| English description... | ... expressed in set notation |
|---|---|
| 3 x | 3x |
| such that | | |
| x must be a natural number | x ∈ N |
| 3x must be smaller than 5,000 | 3x < 5000 |
Well Known Sets
- Natural numbers N= {0, 1, 2, 3, …}
- Integers Z= {…, -2, -1, 0, 1, 2, …}
- Positive Integers Z+= {1, 2, 3, 4, …}
- Real Numbers R= {47.3, -12, π, …}
- Rational Numbers Q= {1.5, 2.6, -3.8, 15, …}
- An Ordinal Number is a number that tells the position of something in a list, such as 1st, 2nd, 3rd, 4th, 5th etc.