Difference between revisions of "Trees"
Mfrederick (talk | contribs) (→Example) |
Mfrederick (talk | contribs) (→What is a Binary Tree Search) |
||
| Line 33: | Line 33: | ||
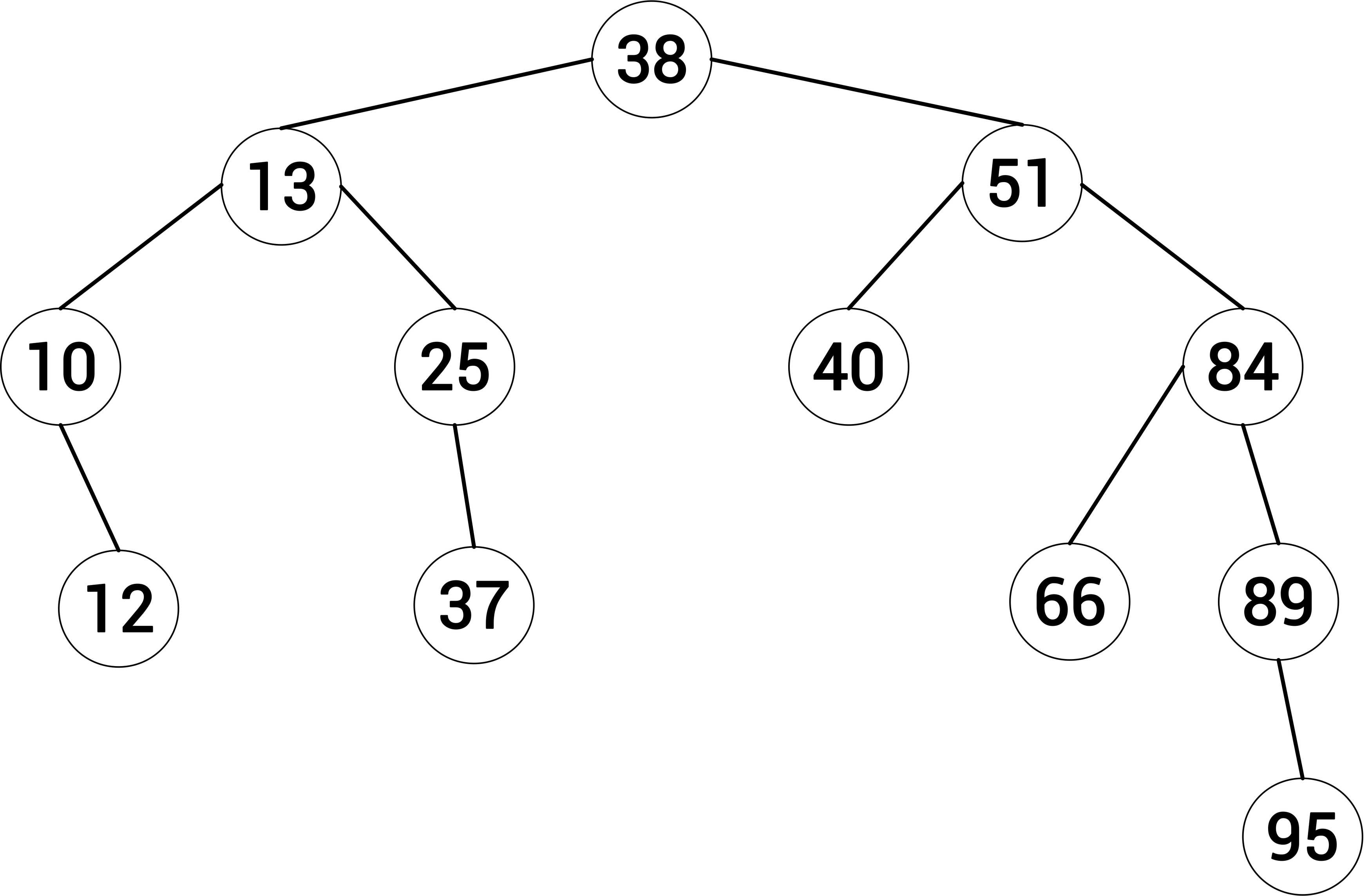
The tree below shows the insertion of: 38, 13, 51, 10, 12, 40, 84, 25, 89, 37, 66, 95 (added in this order) | The tree below shows the insertion of: 38, 13, 51, 10, 12, 40, 84, 25, 89, 37, 66, 95 (added in this order) | ||
| − | [[File:Trees-2.jpg | + | [[File:Trees-2.jpg]] |
The search phase is very similar, you start with the number you wish to find and compare it to the root. Travel from node to node using the rules: | The search phase is very similar, you start with the number you wish to find and compare it to the root. Travel from node to node using the rules: | ||
Revision as of 12:26, 3 December 2017
Contents
What is a Tree
A tree is a connected, undirected graph with no cycles in it.
Connected
All nodes must be connected to other nodes so that no part of the graph is separated. An unconnected graph is essentially 2 separate graphs.
Undirected
A tree can't have any directed edges/arcs. This will be an arrow on the edge/arc to indicate the direction of travel.
No Cycles
A run of interconnected nodes that return to the point of origin.
What is a Rooted Tree
A tree with one vertex singled out as a starting point.
What is a Binary Tree
A binary tree is a graph with no cycles in which each node is succeeded by a maximum of 2 nodes, a 'left' child and a 'right' child, therefore they can be either directed or undirected.
What is a Binary Tree Search
A binary tree can be created from a list of data:
- The first item in the list will be the root of your tree.
- You will then add an item to the tree by firstly comparing the new item to the root.
- If it is alphabetically Lower than the root the new item will be placed on the left of the root.
- If it is alphabetically Higher than the root the new item will be place to the right of the root.
- The next item in the list will again be compared to the root.
- If it is alphabetically Lower than the root the new item will be placed on the left of the root. If the root already has a node to the left, the new item will be compared to this node as well.
- If it is alphabetically Higher than the root the new item will be place to the right of the root. If the root already has a node to the Right, the new item will be compared to this node as well.
Example
The tree below shows the insertion of: 38, 13, 51, 10, 12, 40, 84, 25, 89, 37, 66, 95 (added in this order)
The search phase is very similar, you start with the number you wish to find and compare it to the root. Travel from node to node using the rules:
- Compare the search value with the node, if they are not equal:
- If it is alphabetically Lower than the node travel to the left of the node.
- If it is alphabetically Higher than the node travel to the right of the node.
- If you reach a point and no path can be taken then the item is not in the list.