Difference between revisions of "Graphs"
Mfrederick (talk | contribs) (→Adjacency List) |
Mfrederick (talk | contribs) (→Adjacency Matrix) |
||
| Line 18: | Line 18: | ||
[[File:Graph-2.jpg|thumb|300px]] | [[File:Graph-2.jpg|thumb|300px]] | ||
An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other. | An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
==Adjacency List== | ==Adjacency List== | ||
Revision as of 13:11, 26 November 2017
Contents
What is a graph
A graph is an abstract data structure. It can be used to solve routine problems.
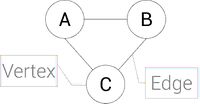
Vertices connected by an edge (see picture) are called Neighbours.
The degree of a vertex is how many things are connected to it, in the picture, there would be 2.
Edges can also be called connectors and vertex can also be called nodes or entries.
Terms
weighted graph
vertex/node
edge/arc
undirected graph
directed graph
Adjacency Matrix
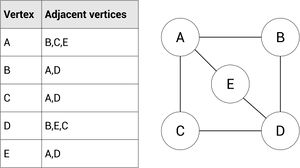
An adjacency matrix is a list showing the what vertexes are connected to their neighbors. This is represented by a list showing what vertex is connected to the other.
Adjacency List
This is a list shown in binary for the values that are going to be connected. It usually helps to transfer the matrices into a list first before you turn it into a graph t make things easier.